Un escalier toutes faces vues
Principe
Suspendus autour d'un cône, cinq escaliers réguliers cherchent leurs points de centre et progressent dans l'espace en s'écartant a minima de la matrice interne. Ce sont des escaliers tournants, hélicoïdaux dans les faits.
L'escalier est toutes faces vues avec fuyantes et contraintes sur
quelques paliers.
Aucun méplat ni faux palier et des raccords strictement bords à bords sont
souhaités.
Les seuls plans horizontaux sont les sous-faces de paliers limitées par
les fuyantes.
Tous les raccords de pente sont épurés.
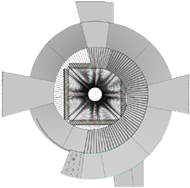
Vue de dessous
Vue représentant toutes les surfaces de tôles ouvragées en sous-face.
(cliquez pour page d'exploration)
La géométrie recherchée pour l'étude et la modélisation
Acte de l'épure et souplesse de mise en oeuvre
Point de dessin paramétrique ou de contraintes sur esquisses comme on modéliserait
sur logiciel paramètrique : ici, dans ce projet, les contraintes sont énumérées
et appliquées par la pensée avant de devenir dessin.
Il aura fallu néanmoins quelques essais, questions au maitre d'oeuvre et
résolutions diverses avant d'élaborer la bonne méthodologie.
Certaines exigences ont conduit à des problèmes récursifs.
Il n'y a finalement qu'un réglage ?
Pour :
- une hauteur de limon et une épaisseur de palier donnés
- une hauteur d'étage
- un angle total d'escalier vu en plan
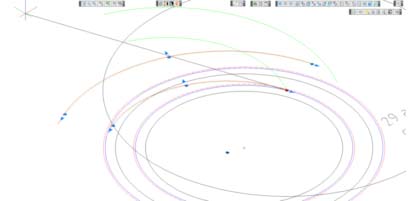
Nous ne recherchons qu'un seule information : la position au plus près du cône.
Tout le reste n'est que contraintes de dessin, c'est ce que nous lirons ici.
Nous rechercherons donc cinq rayons, centres et angles en plan de cinq escaliers les plus proches possbiles du cône.
Moyens CAO mis en oeuvre avec AutoCAD
Notre étude sera basée sur les principe de l'escalier débillardé
régulier : toute section radiale est un rectangle de dimension constante.
Le dessin sera créé en 2D avec ses développés et chacun des étages fera l'objet d'une session de dessin. L'ensemble étant compilé
à l'aide des références externes et les vérifications se faisant grâce à la 3D.
- AutoCAD en 2D et 3D
- Script et programmations Autolisp et VisualLisp
- Routines spécialement écrites pour développés et débillardés de tôles avec 3D
Pas besoin de CAO paramétrique
AutoCAD est une véritable planche à dessin universelle.
La liberté de la mise en oeuvre des contraintes est un atout pour ce projet
Car, qui affirmerait qu'une CAO paramétrique ne serait pas surcontrainte
,
bloquée sur les décisions à prendre et soumise à la dictature de la géométrie naturelle ?
Un tel projet aura donc nécessité la bonne gestion des contraintes à lever
ou à résoudre.
Consultez cet article à propos de l'usage d'
Autolisp
dans l'épure d'un grand projet.
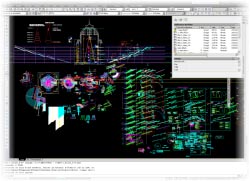
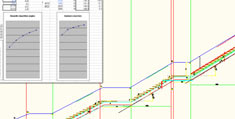
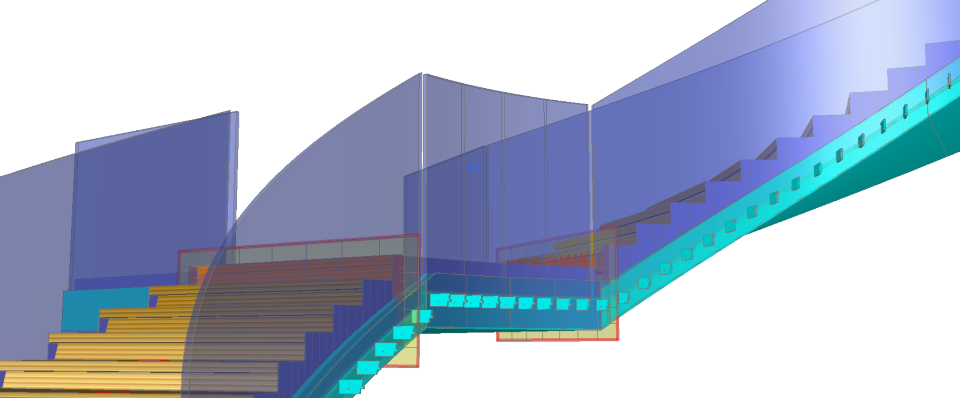
Le dessin d'assemblage de toutes les études peut paraître un peu confus, dans cette vue d'ensemble.
Il est bien organisé pourtant ! Les objets des différents étages s'y superposent.
On découvrira ultérieurement la composition en détail des planches de travail. Il y en a cinq, le nombre d'escaliers et paliers
Une zone du dessin est réservée à la maquette numérique.
Elle permet d'effectuer des vérifications et de dessiner avec précision certains détails.
La vue filaire ci-dessous montre que tous les composants ont été modélisés en 3D
: marches et systèmes, limons roulés et pièces
débillardées.
Une répartition par calques et au sein de blocs permet de se concentrer
sur des pièces particulières. chaque sous-limon possède son calque.
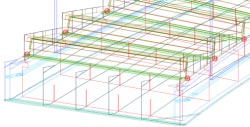
Le travail est en 2D mais il convenait de transformer les escaliers en 3D afin d'effectuer différents types de vérifications et de mesures.
Présentation de l'escalier et données géométriques
01 - Tourner les volées d'escaliers réguliers autour d'un cône
Soit un escalier régulier autour d'un cône.
Si nous progressions autour de celui-ci par le même angle de progression à chaque marche
et pour une même hauteur de marche, à chaque pas notre giron deviendrait
de plus en plus court (puisque le cône nous ressererait).
Il n'existe donc pas d'escalier régulier tournant autour d'un
cône.
C.Q.F.D.
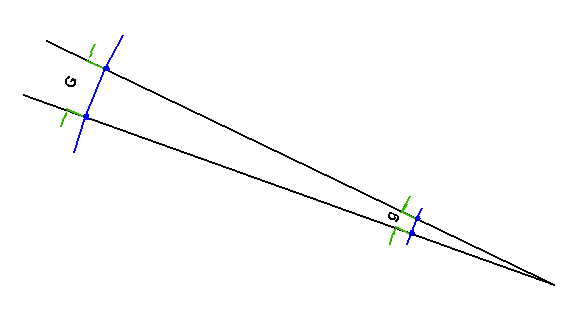
Gérer une banane
Puisqu'il n'y a pas progression régulière, nous projetons de traiter une banane !
Script de la progression courante
Un programme script génère la progression idéale le long du cône.
Ces groupes de lignes, une fois aplatis, donneront, en 2D en plan, la
courbe à suivre au mieux.
Ici, nous avons simplement divisé l'angle total de la foulée de chaque volée
prévue par l'architecte en augmentant Z régulièrement.
Nous créons un ensemble de programmes Autolisp.
Variables globales du projet définissant le cône et les étages
(setq ztop 20830.0; altitude point cône
zbott -10 ; altitude base, révisée à -10mm
Rbott 4050 ; rayon de base du cône
LHt '(2756 2014 2000 2620 2680) ; 5 hauteurs d'étage
Ldiv '(23 15 14 18 18) ; nombre de marche + 1
)Fonction Autolisp exemple renvoyant le rayon du cercle à x altitude
(defun rz(x) (/(* rbott(- ztop x))(- ztop zbott)))
; par exemple
; (rz 2756) -> 3512.46
; (rz -10) -> 4050.0
; (rz 20830.0) -> 0.0
Exagérons le problème posé par le dessin
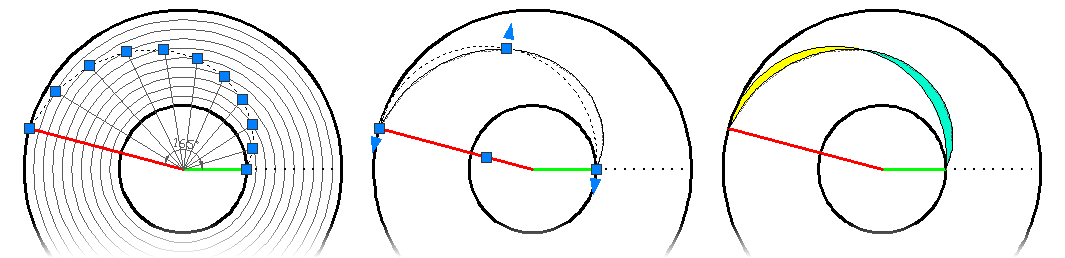
Nous étudions un angle d'escalier en plan proche de 180° et imaginons l'étude
autour d'un cône bien plus aplati (trois fois environ).
Que se passe-t-il alors ?
Sur la deuxième image, nous avons placé un arc de cercle qui passe par
un point intermédiaire, à environ 50% de la progression. C'est ainsi
que seront implantés les escaliers.
Le résultat est une zone faisant s'éloigner l'ouvrage (jaune) suivi d'une
zone le faisant pénétrer le cône (vert-pâle). Il faudra dominer ce paramètre,
bien moins perceptible dans notre cas...
02 - Hauteur de section du limon
L’escalier est un ouvrage continu. A ce titre, le limon intérieur se « déroule » entre volées et paliers.
Puisque l'architecte a conçu chaque volée plus pentue que la précédente,
selon un rythme choisi, les escaliers seront tous différents en girons,
hauteur et hauteurs de marche.
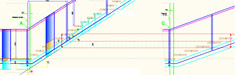
Une hauteur de section de limon selon un principe à choisir
Puisque les pentes sont changeantes entre volées, il faut s'accorder
selon l'un des deux principes dessinés sur l'illustration ci-dessous :
On compare ici le dernier étage, référence minimale de hauteur fournie
par la note de calcul de l'ingénieur et le Rdc, à la
section naturellement plus favorable.
Si la différence parait ténue, les études de pointes (voir plus bas) des
deux cas démontreraient que nos lignes fuyantes glisseraient de :
Différence Y / tan (angle de montée)
avec tan toujours < 1. et proche de 0.4 au premier escalier !
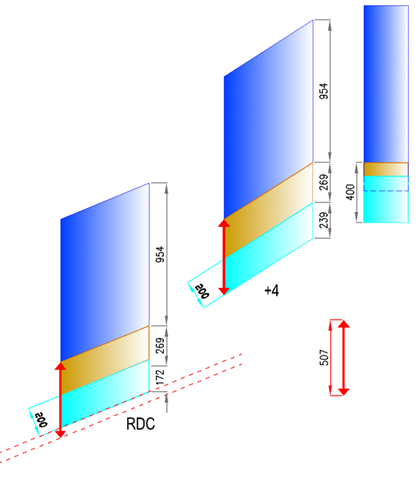
C'est la conservation de la section verticale qui a été choisie
(seconde solution : 262 et 239) par le maître d'oeuvre.
Les paliers, quant à eux, auront tous la même épaisseur de construction,
ce qui est une décision d'autant plus logique à la vue de cette résolution.
La section verticale du palier est, en effet, tout à fait déterminante, nous le
verrons bientôt avec l'étude des pointes.
A chaque volée donc ; son angle
A mesure que l'escalier est gravi par l'usager, l'angle est plus grand,
la pente plus forte, le rythme s'accélère.
Le développé général permet de garder le contrôle même si chacune des
volées fera l'objet d'une étude séparée.
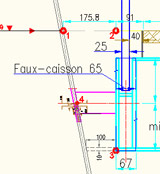
Faux-caisson pour développer les vitrages
Le faux-caisson vaut 65 mm en largeur. Le vrai en ferait 67 car l'un des deux flancs roulés est plus épais.Il place la fibre neutre du vitrage à 32.5 mm du nu intérieur limon, lui-même proche, au point n°3 de + ou - 100 mm du cône. Cette figure mathématique vaudra pour l'ensemble de l'ouvrage et servira différents algorithmes de nos programmes.
Hauteur des faux-caissons internes et externes
Report de la hauteur de conservation pour un débillardé droit et régulier
: la hauteur conservée est utilisée sur les deux flancs (interne et externe)
de l'escalier.
Nous parlons de faux-caisson pour un travail sur la fibre neutre du verre
roulé. Le caisson est dit "faux" car il n'a pas de réalité physique dans
la partie acier, il sera décrit plus loin. La hauteur est, de toutes façons,
conservée dans toute la tranche verticale, le faux-caisson n'est qu'un
concept.
03 - Quelques problèmes posés
Pas d'approximations sur la chaîne de cotes des hauteurs à monter (hauteurs d'étages nettes):
- La moindre variation d'altitude change le plan, ce qui n'est pas courant dans une étude d'escalier.
- Les escaliers sont donc dépendants d'étage à étage mais aussi de l'altitude de ceux-ci ! Il faut s'assurer, au plus près selon l'avancée du chantier, de pouvoir valider définitivement la chaîne de hauteurs. Aucun compromis n'est souhaitable.
Conserver au mieux les angles totaux de chaque volée dessinée par l'architecte
Le dessin originel ouvre, à chaque volée, un angle au sol que nous avons
conservé au mieux.
La distance au cône de du flanc des marches est désormais soumise à la
section résultante calculée verticalement grâce au dessin de caisson.
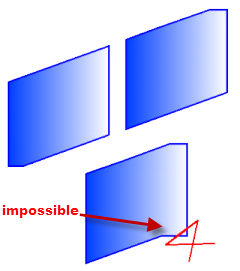
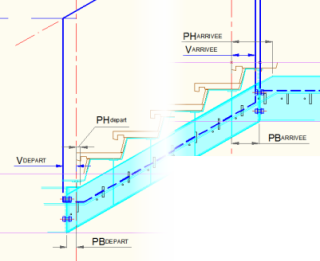
Unifier les rayons de cintrage des éléments en verre.
A chaque jonction entre parties (limon-palier), se produisent trois évènements en pointe :
- La continuité du verre (V)
- Le limon en partie haute (PH)
- Le limon en partie basse (PB)
C'est le limon en partie basse qui pourtant doit rythmer notre développé (PB), ce qui est en contradiction avec le changement de rayon exigé par le verre (V)
PB est fonction de la hauteur de section de la partie acier
PH aussi
V est fonction des hauteurs de garde-corps et rampes
Fort heureusement, les dépassements ne sont pas trop importants (V-PB= proche de 0).
En rouge : des plans de coupe CAO.
Mise en équation du limon continu
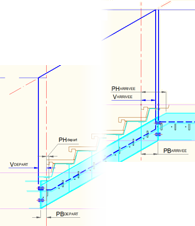
Vdepart + Varrivee = Giron
PHdepart + PHarrivee = Giron
PBdepart + PBarrivee = Giron
Comme il sera vu au point 7 de la page dessin, l'escalier est placé en plan grâce à ce développé et un report proportionnel.
Escalier N, palier et escalier N+1
Quand les pointes deviennent lignes fuyantes majeures
PBdepart et PBarrivee sont désormais les données ultimes
à l'usage du travail en plan.
Devenues lignes directrices fortement contraintes par le chantier (à cause
du pré-scellement pour les paliers), les lignes fuyantes positionnent
définitivement les foulées sur les arcs choisis à chaque escalier. Découvrez
cet enjeu dans les pages suivantes.
Vous explorerez notre méthode de dessin en plan ainsi
que le phénomène de la double-banane dans les pages consacrées
aux haubans.
